Une nouvelle approche de la réfraction subjective
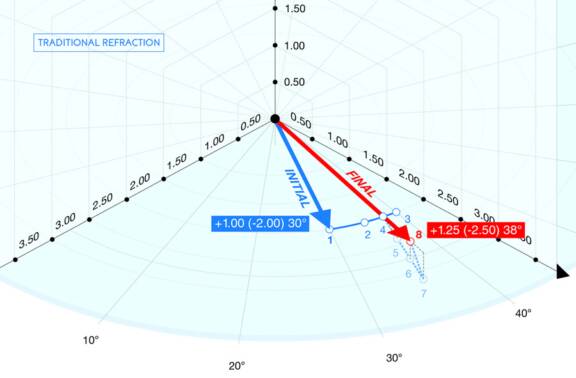
Avec l’avènement des réfracteurs à variations continues de puissances, de nouvelles techniques de mesure de la réfraction subjective peuvent désormais être proposées. L’une d’entre elles consiste en la recherche de la réfraction d’un patient au moyen d’algorithmes semi-automatisés utilisant des changements simultanés de la sphère, du cylindre et de l’axe, et des pas de variations des puissances de dimensions variables*. Cet article en présente les principes généraux et montre comment la détermination de la réfraction peut être rendue plus précise mais aussi plus facile à réaliser par le praticien.