Réfraction : une méthode vectorielle de détermination du cylindre (1/2)
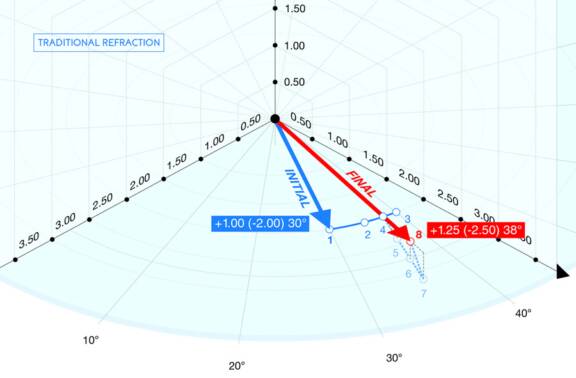
La technique de réfraction utilisée pour la recherche du cylindre a peu évolué depuis longtemps, en raison des limites imposées par les réfracteurs subjectifs utilisant des verres par pas de 0,25 D. Aujourd’hui, avec les réfracteurs à variations continues de puissances* permettant d’agir simultanément sur la sphère, le cylindre et l’axe de la correction, avec une résolution de 0,01 D, il est possible de développer de nouvelles techniques de réfraction subjective. Ce premier article décrit les principes d’une nouvelle technique vectorielle utilisée pour la détermination de l’axe et de la puissance du cylindre. Il sera suivi d’un second article présentant la méthode de réfraction correspondante et la logique d’un algorithme automatisé de recherche du cylindre qui lui est associée.