Réfraction : une méthode vectorielle de détermination du cylindre (2/2)
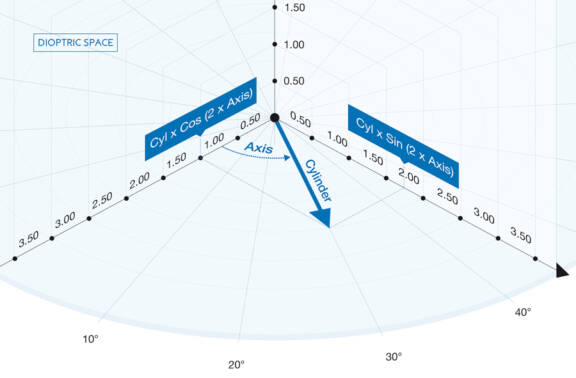
Avec le développement des réfracteurs subjectifs à variations continues de puissance*, une nouvelle approche vectorielle de la recherche du cylindre est rendue possible. Pour faire suite à un premier article décrivant les principes utilisés pour la recherche de l’axe et de la puissance du cylindre [1], ce second article présente la logique d’une méthode vectorielle de détermination du cylindre en la comparant avec la méthode de la réfraction traditionnelle. Il décrit ainsi la logique d’un algorithme automatisé de recherche du cylindre permettant d’assister les praticiens dans leur exercice de la réfraction.